ML-09: K-Nearest Neighbors (KNN)

Publish on: Classify at:
Words: 2366 Read:≈ 12min
Summary
Master the simplest yet powerful classification algorithm: understand distance metrics, the curse of dimensionality, optimal K selection, and implement KNN from scratch with stunning decision boundary visualizations.

Learning Objectives

  • Understand the KNN algorithm and instance-based learning
  • Master common distance metrics
  • Learn how to choose the optimal K value
  • Recognize the curse of dimensionality

Theory

What is K-Nearest Neighbors?

K-Nearest Neighbors (KNN) is one of the simplest and most intuitive machine learning algorithms. Unlike models that learn complex decision boundaries, KNN makes predictions based on a simple principle:

To classify a new point, find its K closest neighbors and let them vote.

graph LR
    A["❓ New Point"] --> B["Find K=3 Nearest Neighbors"]
    B --> C["🔵 Neighbor 1: Class A"]
    B --> D["🔵 Neighbor 2: Class A"]
    B --> E["🔴 Neighbor 3: Class B"]
    C --> F["🗳️ Vote: 2A vs 1B"]
    D --> F
    E --> F
    F --> G["✅ Predict: Class A"]
    
    style G fill:#c8e6c9

Lazy Learning vs Eager Learning

KNN is a lazy learner (also called instance-based learning):

AspectLazy Learning (KNN)Eager Learning (Logistic Regression, SVM)
TrainingJust store the dataBuild a model from data
PredictionCompute distances at query timeUse pre-built model
MemoryStores entire datasetStores only model parameters
AdaptabilityEasy to add new dataNeed to retrain
No explicit training phase! KNN simply memorizes all training examples. All the work happens during prediction.

Distance Metrics

Since KNN relies on finding the “nearest” neighbors, how we measure distance between points is crucial. The choice of distance metric can significantly impact model performance.

Euclidean Distance (L2)

The most common metric — straight-line distance in n-dimensional space:

$$d(x, y) = \sqrt{\sum_{i=1}^{n} (x_i - y_i)^2}$$

Example$x$$y$Distance
2D(0, 0)(3, 4)$\sqrt{9 + 16} = 5$
3D(1, 2, 3)(4, 6, 3)$\sqrt{9 + 16 + 0} = 5$

Manhattan Distance (L1)

Sum of absolute differences — distance along grid lines:

$$d(x, y) = \sum_{i=1}^{n} |x_i - y_i|$$

Example$x$$y$Distance
2D(0, 0)(3, 4)$|3| + |4| = 7$
When to use Manhattan? When features are on different scales or when movement is restricted to axes (like city blocks).

Chebyshev Distance (L∞)

The maximum absolute difference across any dimension:

$$d(x, y) = \max_{i} |x_i - y_i|$$

Example$x$$y$Distance
2D(0, 0)(3, 4)$\max(3, 4) = 4$
When to use Chebyshev? When the largest single difference matters most, like a king’s movement in chess (can move diagonally in one step).

Minkowski Distance (Generalized)

Euclidean, Manhattan, and Chebyshev are all special cases of the Minkowski distance:

$$d(x, y) = \left(\sum_{i=1}^{n} |x_i - y_i|^p\right)^{1/p}$$

$p$NameUnit Ball ShapeDescription
1Manhattan (L1)◇ DiamondSum of absolute differences
2Euclidean (L2)○ CircleStraight-line distance
∞Chebyshev (L∞)□ SquareMaximum single difference
Unit Ball Shape refers to the contour of all points at distance = 1 from the origin. This visualizes how each metric defines “equal distance”.
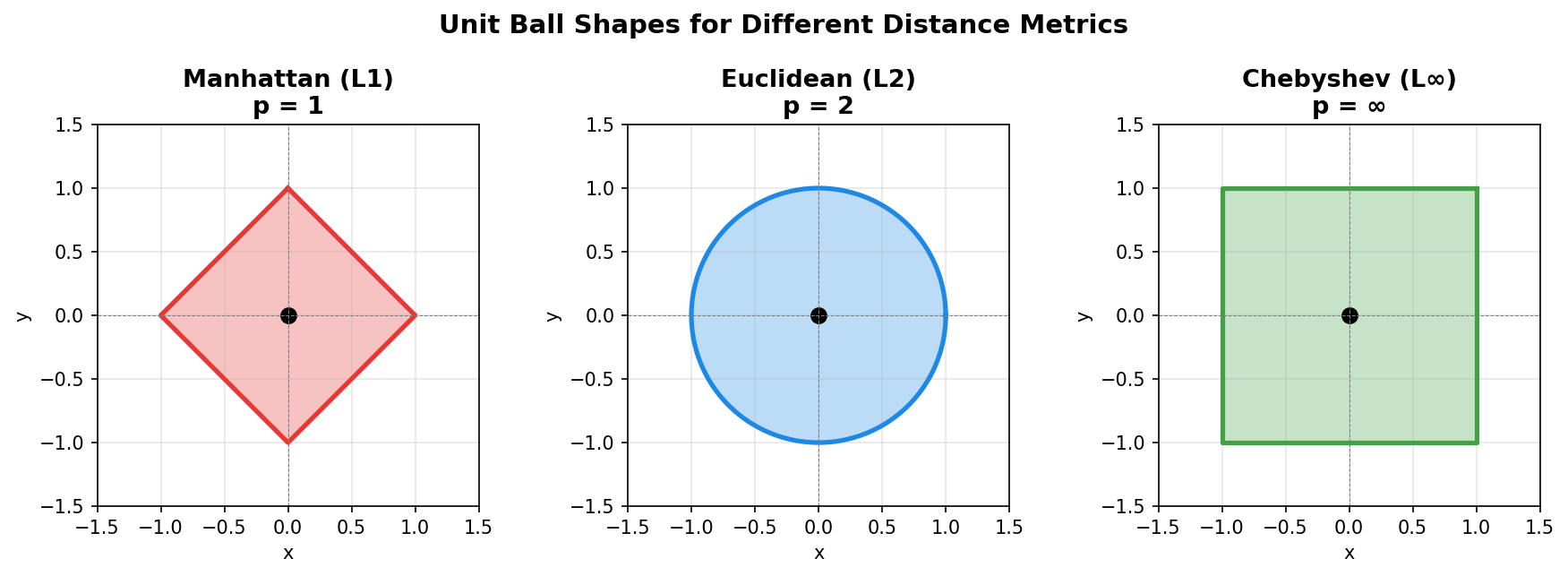
Unit ball shapes for Manhattan, Euclidean, and Chebyshev distances
Unit ball shapes: Manhattan forms a diamond (rotated square), Euclidean forms a circle, and Chebyshev forms a square. Points on each boundary are equidistant from the origin under their respective metrics.

Comparison

MetricBest ForSensitivity to Outliers
EuclideanDefault choice, continuous featuresHigh
ManhattanHigh-dimensional, sparse dataLower
ChebyshevWhen max difference mattersVery high

The KNN Algorithm

With distance metrics covered, the next step is to see how KNN uses them to make predictions:

Input: Training data ${(x_1, y_1), …, (x_N, y_N)}$, query point $x_q$, number of neighbors $K$

Algorithm:

  1. Compute distance from $x_q$ to all training points
  2. Sort by distance (ascending)
  3. Select the $K$ nearest neighbors
  4. Classification: Return majority class among neighbors
  5. Regression: Return average (or weighted average) of neighbor values
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

function KNN_Classify(X_train, y_train, x_query, K):
    distances = []
    for i = 1 to N:
        d = distance(x_query, X_train[i])
        distances.append((d, y_train[i]))
    
    distances.sort()  # Sort by distance
    
    neighbors = distances[:K]  # Take K nearest
    
    return majority_vote(neighbors)

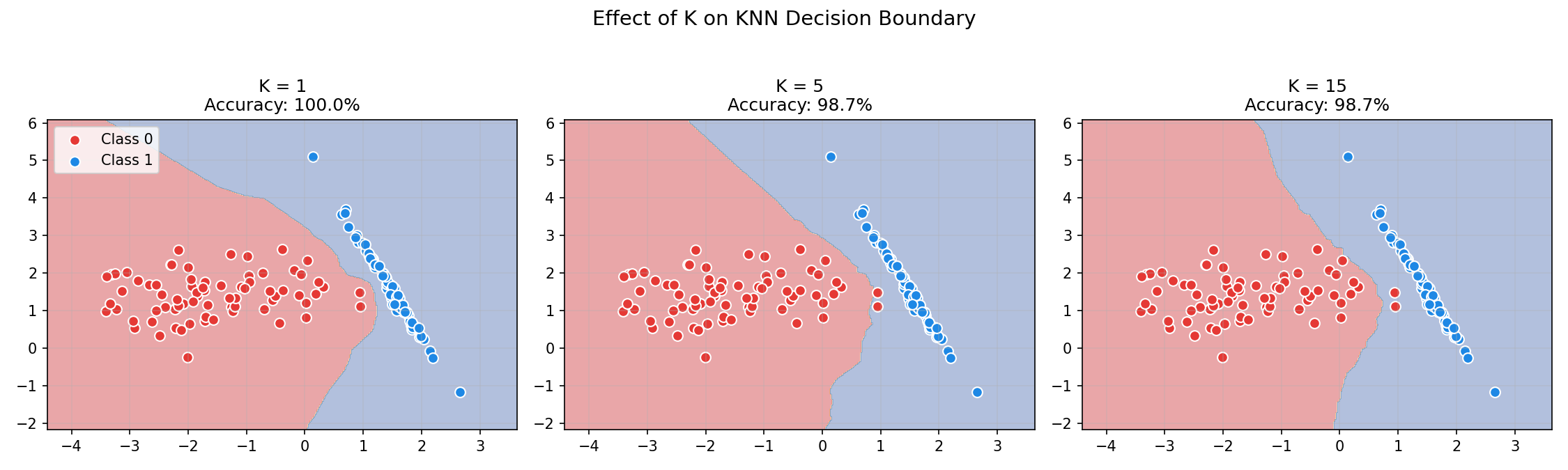
Choosing K: The Bias-Variance Tradeoff

The choice of $K$ dramatically affects model behavior:

K ValueBehaviorRisk
K = 1Very flexible, follows training data closelyOverfitting — sensitive to noise
K = NPredicts majority class for everythingUnderfitting — ignores local structure
K = √NRule of thumb starting pointBalance

Practical guidelines:

  • Use odd K for binary classification (avoids ties)
  • Start with $K = \sqrt{N}$ or $K = 5$
  • Cross-validate to find optimal K
  • Typical range: 1-20

Weighted KNN

In standard KNN, all K neighbors have equal influence on the prediction. But intuitively, closer neighbors should matter more — this is the idea behind Weighted KNN:

$$\hat{y} = \frac{\sum_{i \in N_K} w_i \cdot y_i}{\sum_{i \in N_K} w_i}$$

where $w_i = \frac{1}{d(x_q, x_i)^2}$ (inverse distance weighting)

MethodCloser NeighborsFarther Neighbors
UniformSame weightSame weight
Distance-weightedHigh weightLow weight

The Curse of Dimensionality

KNN works beautifully in low dimensions, but faces serious challenges as the number of features grows. This is known as the curse of dimensionality:

  1. Distances become meaningless: In high dimensions, all points become roughly equidistant
  2. Data becomes sparse: Need exponentially more data to cover the space
  3. Computation explodes: $O(N \cdot d)$ for each query
DimensionsPoints needed to fill spaceNearest neighbor reliability
2D100✅ Good
10D$10^{10}$⚠️ Degraded
100D$10^{100}$❌ Meaningless

Solutions:

  • Reduce dimensions (PCA, t-SNE)
  • Use feature selection
  • Consider other algorithms for $d > 20$

Code Practice

This section implements KNN from scratch, then demonstrates sklearn for real-world applications.

KNN from Scratch

🐍 Python
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

import numpy as np
from collections import Counter

class KNNClassifier:
    def __init__(self, k=3, metric='euclidean'):
        self.k = k
        self.metric = metric
    
    def fit(self, X, y):
        """Store training data (lazy learning!)"""
        self.X_train = np.array(X)
        self.y_train = np.array(y)
        return self
    
    def _distance(self, x1, x2):
        """Compute distance between two points."""
        if self.metric == 'euclidean':
            return np.sqrt(np.sum((x1 - x2) ** 2))
        elif self.metric == 'manhattan':
            return np.sum(np.abs(x1 - x2))
    
    def _predict_one(self, x):
        """Predict class for a single sample."""
        # Compute distances to all training points
        distances = [self._distance(x, x_train) for x_train in self.X_train]
        
        # Get indices of K nearest neighbors
        k_indices = np.argsort(distances)[:self.k]
        
        # Get labels of K nearest neighbors
        k_labels = self.y_train[k_indices]
        
        # Return majority vote
        return Counter(k_labels).most_common(1)[0][0]
    
    def predict(self, X):
        """Predict classes for all samples."""
        return np.array([self._predict_one(x) for x in X])
    
    def score(self, X, y):
        """Compute accuracy."""
        return np.mean(self.predict(X) == y)


# Test with Iris dataset
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

knn = KNNClassifier(k=5)
knn.fit(X_train, y_train)

print(f"Training samples: {len(X_train)}")
print(f"Test accuracy: {knn.score(X_test, y_test):.2%}")

Output:

1
2

Training samples: 120
Test accuracy: 100.00%

sklearn KNN Example

🐍 Python
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, cross_val_score

# Load data
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

# Train KNN
knn = KNeighborsClassifier(n_neighbors=5, metric='euclidean')
knn.fit(X_train, y_train)

# Evaluate
train_acc = knn.score(X_train, y_train)
test_acc = knn.score(X_test, y_test)
cv_scores = cross_val_score(knn, X, y, cv=5)

print("📊 KNN Performance on Iris Dataset")
print("=" * 40)
print(f"Train accuracy:      {train_acc:.2%}")
print(f"Test accuracy:       {test_acc:.2%}")
print(f"Cross-val accuracy:  {cv_scores.mean():.2%} ± {cv_scores.std():.2%}")

Output:

1
2
3
4
5

📊 KNN Performance on Iris Dataset
========================================
Train accuracy:      96.67%
Test accuracy:       100.00%
Cross-val accuracy:  97.33% ± 2.49%

Finding Optimal K with Cross-Validation

🐍 Python
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import cross_val_score

# Test different K values
k_range = range(1, 31)
cv_scores = []

for k in k_range:
    knn = KNeighborsClassifier(n_neighbors=k)
    scores = cross_val_score(knn, X, y, cv=5, scoring='accuracy')
    cv_scores.append(scores.mean())

# Find optimal K
optimal_k = k_range[np.argmax(cv_scores)]
best_score = max(cv_scores)

print(f"🎯 Optimal K: {optimal_k}")
print(f"📈 Best CV Score: {best_score:.2%}")
print(f"\n📊 Top 5 K values:")
for k, score in sorted(zip(k_range, cv_scores), key=lambda x: -x[1])[:5]:
    print(f"   K={k:2d}: {score:.2%}")

Output:

1
2
3
4
5
6
7
8
9

🎯 Optimal K: 6
📈 Best CV Score: 98.00%

📊 Top 5 K values:
   K= 6: 98.00%
   K= 7: 98.00%
   K=10: 98.00%
   K=11: 98.00%
   K=12: 98.00%

Decision Boundary Visualization

🐍 Python
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import make_classification

# Generate 2D data for visualization
np.random.seed(42)
X, y = make_classification(
    n_samples=150, n_features=2, n_redundant=0,
    n_informative=2, n_clusters_per_class=1, 
    class_sep=1.5, random_state=42
)

fig, axes = plt.subplots(1, 3, figsize=(15, 4.5))
k_values = [1, 5, 15]

for ax, k in zip(axes, k_values):
    # Train KNN
    knn = KNeighborsClassifier(n_neighbors=k)
    knn.fit(X, y)
    
    # Create mesh grid
    h = 0.02
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))
    
    # Predict on mesh
    Z = knn.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    
    # Plot decision boundary
    ax.contourf(xx, yy, Z, alpha=0.4, cmap='RdYlBu')
    ax.scatter(X[y==0, 0], X[y==0, 1], c='#E53935', s=50, 
               edgecolors='white', label='Class 0')
    ax.scatter(X[y==1, 0], X[y==1, 1], c='#1E88E5', s=50, 
               edgecolors='white', label='Class 1')
    
    acc = knn.score(X, y)
    ax.set_title(f'K = {k}\nAccuracy: {acc:.1%}', fontsize=12)
    ax.grid(True, alpha=0.3)

axes[0].legend(loc='upper left')
fig.suptitle('Effect of K on KNN Decision Boundary', fontsize=14)
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.savefig('assets/knn_decision_boundary.png', dpi=150)
plt.show()
KNN decision boundaries for different K values
Effect of K on decision boundary: K=1 creates a very complex boundary that follows each point (overfitting), K=5 is balanced, K=15 produces a smoother boundary.

Distance Metrics Comparison

🐍 Python
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler

# Scale features (important for KNN!)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
X_train_s, X_test_s, y_train, y_test = train_test_split(
    X_scaled, y, test_size=0.2, random_state=42
)

print("📊 Distance Metric Comparison")
print("=" * 50)
print(f"{'Metric':<15} {'Train Acc':>12} {'Test Acc':>12}")
print("-" * 50)

for metric in ['euclidean', 'manhattan', 'chebyshev', 'minkowski']:
    knn = KNeighborsClassifier(n_neighbors=5, metric=metric)
    knn.fit(X_train_s, y_train)
    
    train_acc = knn.score(X_train_s, y_train)
    test_acc = knn.score(X_test_s, y_test)
    
    print(f"{metric:<15} {train_acc:>12.2%} {test_acc:>12.2%}")

Output:

1
2
3
4
5
6
7
8

📊 Distance Metric Comparison
==================================================
Metric             Train Acc     Test Acc
--------------------------------------------------
euclidean             98.33%      100.00%
manhattan             99.17%      100.00%
chebyshev             98.33%      100.00%
minkowski             98.33%      100.00%

Deep Dive

Here are answers to common questions about KNN that often come up in practice.

Frequently Asked Questions

Q1: Should I scale features before KNN?

Yes, absolutely! KNN is distance-based, so features on larger scales dominate.

Feature ScalingImpact on KNN
Not scaledFeatures with larger range dominate distance
StandardScalerZero mean, unit variance — equal contribution
MinMaxScaler[0, 1] range — also works well
1
2
3
4
5

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)  # Use same scaler!
Always fit the scaler on training data only, then transform both train and test sets.

Q2: KNN vs other classifiers — when to use which?

ScenarioRecommendationWhy
Small dataset, few featuresKNNSimple, effective
Large dataset (N > 100k)Logistic Regression, Random ForestKNN is too slow
High-dimensional (d > 20)SVM, Random ForestCurse of dimensionality
Need probability outputsLogistic RegressionKNN probabilities are rough
Non-linear boundariesKNN, SVM (RBF)KNN handles complex shapes
Interpretability neededDecision TreeKNN is hard to explain

Q3: How to speed up KNN?

MethodDescriptionSpeedup
KD-TreeTree structure for nearest neighbor search10-100x
Ball TreeWorks better in higher dimensions10-100x
Approximate NNTrade accuracy for speed (Annoy, FAISS)100-1000x
Reduce dimensionsPCA before KNNDepends on compression
1
2
3
4
5

# sklearn automatically chooses algorithm
knn = KNeighborsClassifier(n_neighbors=5, algorithm='auto')

# Force specific algorithm
knn = KNeighborsClassifier(n_neighbors=5, algorithm='kd_tree')

Q4: KNN for regression?

KNN works for regression too — just average the neighbor values:

$$\hat{y} = \frac{1}{K} \sum_{i \in N_K} y_i$$

1
2
3
4
5

from sklearn.neighbors import KNeighborsRegressor

reg = KNeighborsRegressor(n_neighbors=5, weights='distance')
reg.fit(X_train, y_train)
predictions = reg.predict(X_test)

Q5: How to handle ties in voting?

StrategyDescription
Use odd KFor binary classification, avoids ties
Random selectionPick randomly among tied classes
Weight by distanceCloser points break the tie
Increase KUntil tie is broken

sklearn uses random selection for ties by default.

Practical Tips

KNN Checklist:

  1. Scale features — always!
  2. Start with K=5 and cross-validate
  3. Use odd K for binary problems
  4. Consider weighted voting for imbalanced data
  5. Check dimensions — avoid d > 20

Common Pitfalls

PitfallSymptomSolution
Unscaled featuresPoor accuracy, one feature dominatesUse StandardScaler
Too small KOverfitting, noisy predictionsIncrease K
Too large KUnderfitting, ignores local patternsDecrease K
High dimensionsSlow, poor accuracyReduce dimensions
Imbalanced classesPredicts majority classUse weighted KNN
Slow predictionLarge N or dUse KD-tree, reduce data

Summary

Key Formulas

ConceptFormula
Euclidean Distance$d(x, y) = \sqrt{\sum_i (x_i - y_i)^2}$
Manhattan Distance$d(x, y) = \sum_i |x_i - y_i|$
Classification$\hat{y} = \text{mode}(y_{N_K})$
Regression$\hat{y} = \frac{1}{K} \sum_{i \in N_K} y_i$

Key Takeaways

  1. KNN is instance-based — no training, all work at prediction time
  2. Distance metrics matter — Euclidean is default, Manhattan for sparse data
  3. K controls complexity — small K overfits, large K underfits
  4. Feature scaling is essential — unscaled features break KNN
  5. Curse of dimensionality — KNN struggles in high dimensions
  6. Simple but powerful — excellent baseline, competitive on small datasets

When to Use KNN

✅ Use When❌ Avoid When
Small dataset (N < 10k)Large dataset (N > 100k)
Low dimensions (d < 20)High dimensions (d > 50)
Non-linear patternsLinear relationships
Quick baseline neededFast prediction required
Memory is availableMemory constrained

References

  • Cover, T. & Hart, P. (1967). “Nearest Neighbor Pattern Classification”
  • sklearn KNeighborsClassifier
  • Hastie, T. et al. “The Elements of Statistical Learning” - Chapter 13
  • Beyer, K. et al. (1999). “When Is ‘Nearest Neighbor’ Meaningful?”